数据结构
线性数据结构:数组、链表、栈、队列、哈希表,元素之间是一对一的顺序关系非线性数据结构:树、堆、图、哈希表
树形结构:树、堆、哈希表,元素之间是一对多的关系网状结构:图,元素之间是多对多的关系
数组
逻辑顺序与物理顺序一致,均线性,将相同类型的元素存储在连续的内存空间中。索引本质上是
内存地址的偏移量,从 0 开始
访问元素:O(1),给定数组内存地址(首元素内存地址)和某个元素的索引,直接访问该元素 =>
元素内存地址 = 数组内存地址 + 元素长度 * 索引1
2
3
4
5数组:[1, 3, 2, 5, 4]
索引: 0 1 2 3 4
地址:00 04 08 12 16
长度:4
索引 3 处的元素地址:000 + 4 * 3 = 012插入元素:O(n),插入一个元素,需要将该元素之后的所有元素都向后移动一位,之后再把元素赋值给该索引。由于数组的长度不可变,插入元素后,超出数组长度范围的元素会丢失
删除元素:O(n),删除索引 i 处的元素,需要把索引 i 之后的元素都向前移动一位
扩容元素:O(n),在复杂的系统环境中,程序难以保证数组之后的内存空间是可用的,无法安全地扩展数组容量。因此在大多数编程语言中,数组的长度是不可变的。如需扩容数组,需重新建立一个更大的数组,然后把原数组元素依次复制到新数组
链表
物理上非线性,元素在内存中分散存储,但通过指针的逻辑连接形成线性关系。每个节点包含
数据域(元素值)和指针域(指向后继结点,最后一个为 null)。双向链表指针域包含前驱和后继。环形链表尾节点指向头节点
访问元素:O(n),从头节点遍历访问
插入元素:O(1),改变两个节点指针即可
删除元素:O(1),改变一个节点指针即可。尽管改变之后被删除节点指针仍指向存活元素,但已经无法线性访问到
典型应用
单向链表
栈与队列:当插入和删除操作都在链表的一端进行时,先进后出,对应栈;当插入操作在链表的一端进行,删除操作在链表的另一端进行,先进先出,对应队列
哈希表:解决哈希冲突,所有冲突的元素都会被放到一个链表中
图:邻接表是表示图的一种常用方式,其中图的每个顶点都与一个链表相关联,链表中的每个元素都代表与该顶点相连的其他顶点
双向链表
高级数据结构:比如在红黑树、B 树中,需要访问节点的父节点,通过在节点中保存一个指向父节点的引用来实现,类似于双向链表
浏览器历史:在网页浏览器中,当用户点击前进或后退按钮时,浏览器需要知道用户访问过的前一个和后一个网页
LRU 算法:在缓存淘汰(LRU)算法中,需要快速找到最近最少使用的数据,以及支持快速添加和删除节点
环形链表
时间片轮转调度算法:在操作系统中,时间片轮转调度算法是一种常见的 CPU 调度算法,它需要对一组进程进行循环。每个进程被赋予一个时间片,当时间片用完时,CPU 将切换到下一个进程
数据缓冲区:在某些数据缓冲区的实现中,也可能会使用环形链表。比如在音频、视频播放器中,数据流可能会被分成多个缓冲块并放入一个环形链表,以便实现无缝播放
栈
一种遵循先入后出逻辑的线性数据结构
队列
一种遵循先入先出逻辑的线性数据结构
哈希表
散列表,通过建立键 key 与值 value 之间的映射,实现高效的元素查询
哈希算法
特点:确定性、效率高、均匀分布
安全特性:单向性 (无法反推输入信息)、抗碰撞性 (极难找到两个不同的输入有相同输出)、雪崩效应 (输入的微小变化应当导致输出的显著且不可预测的变化)
密码学要求:加盐
最常用
除留余数法:将键值对哈希表的大小 m 取模,直接得到索引
1
2
3hash(key) = key % m
// 优化:高 16 位与低 16 位异或,打破高位冗余,高位变化小而低位重复时,通过位运算增强随机性
hash(key) = (key ^ (key >> 16)) % m- 适合键值为整数的场景
- m 通常选择质数(如 31、101、1009),避免因键值存在周期性(如偶数键)导致哈希值集中在少数索引
- 优化建议:
位运算哈希。通过位移、异或等操作打乱键的二进制位,再取模
乘法哈希:通过常数乘法和位移操作映射索引
1
hash(key) = floor(m × (key × A mod 1))
- A 是 (√5 - 1)/2 ≈ 0.618(黄金比例的小数部分),m 为哈希表大小(通常是 2 的幂)
- 无需选质数 m,计算仅需乘法和位移,速度极快,适合对性能要求极高的场景
字符串哈希函数
字符串需先转换为整数再映射,核心是让不同字符串的整数表示尽可能唯一,避免哈希碰撞
多项式滚动哈希:将字符串视为某个基数 base 的多项式,按字符 ASCII 值计算,对字符串
s = s₀s₁...sₙ₋₁,hash(s) = (s₀×baseⁿ⁻¹ + s₁×baseⁿ⁻² + ... + sₙ₋₁×base⁰) mod m- base 通常取质数(如 31、127、911),减少字符映射的重复性
- m 取大质数(如
10⁹+7),降低碰撞概率 - 支持增量计算(新增字符时只需 hash = hash×base + new_char)
- 适合动态字符串哈希(如哈希表中字符串的插入 / 查询)
1
2// 字符串 "abc"(ASCII 值 97,98,99),base=31 时
hash = (97×31² + 98×31 + 99) mod m = (97×961 + 98×31 + 99) mod m = 99624 mod mDJB2 哈希
- hash = 5381(初始值),对每个字符 c:hash = hash×33 + c,最后取模哈希表大小
- 计算简单(仅乘法和加法),分布均匀,广泛用于哈希表(如 PHP 的数组哈希实现)
FNV 哈希(Fowler-Noll-Vo):基于 “异或” 和 “乘法” 的混合操作
- 分布均匀性极佳,计算速度快,适合哈希表和缓存系统
哈希冲突
负载因子:哈希表的元素数量除以桶数量,用于衡量哈希冲突的严重程度,也常作为哈希表扩容的触发条件。
链式地址
在原始哈希表中,每个桶仅能存储一个键值对。链式地址(separate chaining)将单个元素转换为链表,将键值对作为链表节点,将所有发生冲突的键值对都存储在同一链表中
- 当链表很长时,查询效率 O(n) 很差。此时可以将链表转换为 “AVL 树” 或 “红黑树”,从而将查询操作的时间复杂度优化至 O(logn)

开放寻址
开放寻址(open addressing)不引入额外的数据结构,通过 “多次探测” 来处理哈希冲突,探测方式主要包括线性探测、平方探测和多次哈希等
线性探测
线性探测采用固定步长的线性搜索来进行探测,其操作方法与普通哈希表有所不同
- 插入元素:通过哈希函数计算桶索引,若发现桶内已有元素,则从冲突位置向后线性遍历(步长通常为 1),直至找到空桶,将元素插入其中
- 查找元素:若发现哈希冲突,则使用相同步长向后进行线性遍历,直到找到对应元素,返回 value 即可;如果遇到空桶,说明目标元素不在哈希表中,返回 None

劣势:
- 容易产生聚集现象:数组中连续被占用的位置越长,这些连续位置发生哈希冲突的可能性越大,从而进一步促使该位置的聚堆生长,形成恶性循环,最终导致增删查改操作效率劣化
- 不能在开放寻址哈希表中直接删除元素:删除元素会在数组内产生一个空桶 None ,而当查询元素时,线性探测到该空桶就会返回,因此在该空桶之下的元素都无法再被访问到,程序可能误判这些元素不存在
改进:
懒删除:利用常量 TOMBSTONE 标记需要删除的桶。在该机制下,None 和 TOMBSTONE 都代表空桶,都可以放置键值对。但不同的是,线性探测到 TOMBSTONE 时应该继续遍历,因为其之下可能还存在键值对
- 然而懒删除可能会加速哈希表的性能退化:每次删除操作都会产生一个删除标记,随着 TOMBSTONE 的增加,搜索时间也会增加,因为线性探测可能需要跳过多个 TOMBSTONE 才能找到目标元素
优化:
在线性探测中记录遇到的首个 TOMBSTONE 的索引,并将搜索到的目标元素与该 TOMBSTONE 交换位置。当每次查询或添加元素时,元素会被移动至距离理想位置(探测起始点)更近的桶,从而优化查询效率
平方探测
与线性探测类似,不同的是跳过 “探测次数的平方” 的步数,即 1, 4, 9,…步
优势:
- 平方探测通过跳过探测次数平方的距离,试图缓解线性探测的聚集效应
- 平方探测会跳过更大的距离来寻找空位置,有助于数据分布得更加均匀
劣势:
- 仍然存在聚集现象,即某些位置比其他位置更容易被占用
- 由于平方的增长,平方探测可能不会探测整个哈希表,这意味着即使哈希表中有空桶,平方探测也可能无法访问到它
多次哈希
使用多个哈希函数进行探测
- 插入元素:若哈希函数 f1(x) 出现冲突,则尝试 f2(x),以此类推,直到找到空位后插入元素
- 查找元素:在相同的哈希函数顺序下进行查找,直到找到目标元素时返回;若遇到空位或已尝试所有哈希函数,说明哈希表中不存在该元素,则返回 None
树
二叉树
- 完美二叉树:也称满二叉树,所有层的节点都被完全填满。在完美二叉树中,叶节点的度为 0,其余所有节点的度都为 2;若树的高度为 h,则节点总数为 2^(h+1) - 1,呈现标准的指数级关系
- 完全二叉树:仅允许最底层的节点不完全填满,且最底层的节点必须从左至右依次连续填充。非常适合用数组来表示,给定索引 i,其左子节点的索引为 2i + 1,右子节点的索引为 2i + 2,父节点的索引为 (i - 1) / 2 (向下整除)。当索引越界时,表示空节点或节点不存在
- 完满二叉树:除了叶节点之外,其余所有节点都有两个子节点
- 平衡二叉树:任意节点的平衡因子(左子树和右子树的高度之差) 的绝对值不超过 1
遍历
层序遍历
广度优先遍历,从顶部到底部逐层遍历二叉树,并在每一层按照从左到右的顺序访问节点。时间/空间复杂度均为 O(n)
1 | function levelOrder(root) { |
前序、中序、后序遍历
深度优先遍历,深度优先遍历就像是绕着整棵二叉树的外围走一圈。时间/空间复杂度均为 O(n)
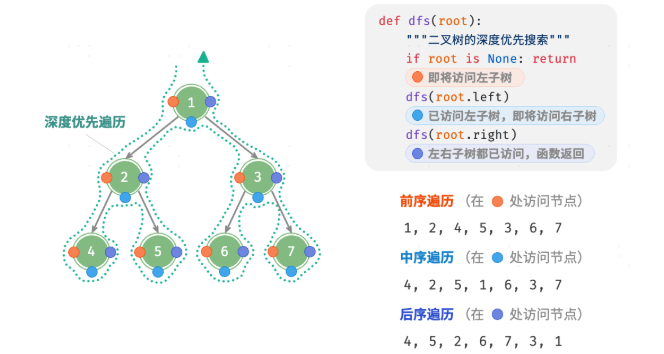
1 | /* 前序遍历 */ |
二叉搜索树
- 对于根节点,左子树中所有节点的值 < 根节点的值 < 右子树中所有节点的值,不允许存在重复节点
- 任意节点的左、右子树也是二叉搜索树,即同样满足条件 1
故有性质:二叉搜索树的中序遍历序列是升序的
查找节点:与二分查找算法的工作原理一致,都是每轮排除一半情况。循环次数最多为二叉树的高度,当二叉树平衡时,使用 O(logn) 时间
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15/* 查找节点 */
search(num) {
let cur = this.root;
// 循环查找,越过叶节点后跳出
while (cur !== null) {
// 目标节点在 cur 的右子树中
if (cur.val < num) cur = cur.right;
// 目标节点在 cur 的左子树中
else if (cur.val > num) cur = cur.left;
// 找到目标节点,跳出循环
else break;
}
// 返回目标节点
return cur;
}插入节点:O(logn)
- 查找插入位置:与查找操作相似,从根节点出发,根据当前节点值和 num 的大小关系循环向下搜索,直到越过叶节点(遍历至 None )时跳出循环
- 在该位置插入节点:初始化节点 num ,将该节点置于 None 的位置
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24/* 插入节点 */
insert(num) {
// 若树为空,则初始化根节点
if (this.root === null) {
this.root = new TreeNode(num);
return;
}
let cur = this.root,
pre = null;
// 循环查找,越过叶节点后跳出
while (cur !== null) {
// 找到重复节点,直接返回
if (cur.val === num) return;
pre = cur;
// 插入位置在 cur 的右子树中
if (cur.val < num) cur = cur.right;
// 插入位置在 cur 的左子树中
else cur = cur.left;
}
// 插入节点
const node = new TreeNode(num);
if (pre.val < num) pre.right = node;
else pre.left = node;
}删除节点:O(logn)
- 当待删除节点的度为 0 时,表示该节点是叶节点,可以直接删除
- 当待删除节点的度为 1 时,将待删除节点替换为其子节点即可
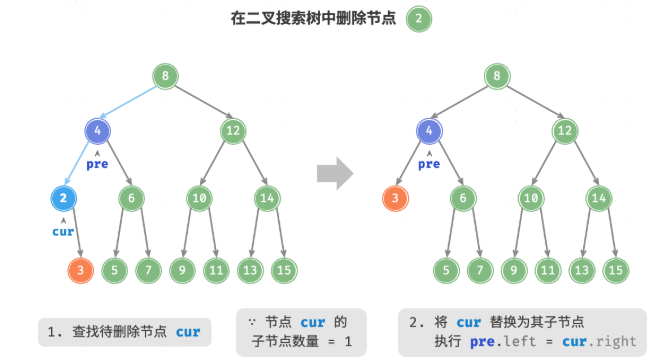
- 当待删除节点的度为 2 时,无法直接删除它,而需要使用一个节点替换该节点。由于要保持二叉搜索树的性质,这个节点可以是
右子树的最小节点或左子树的最大节点
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43remove(num) {
// 若树为空,直接提前返回
if (this.root === null) return;
let cur = this.root,
pre = null;
// 循环查找,越过叶节点后跳出
while (cur !== null) {
// 找到待删除节点,跳出循环
if (cur.val === num) break;
pre = cur;
// 待删除节点在 cur 的右子树中
if (cur.val < num) cur = cur.right;
// 待删除节点在 cur 的左子树中
else cur = cur.left;
}
// 若无待删除节点,则直接返回
if (cur === null) return;
// 子节点数量 = 0 or 1
if (cur.left === null || cur.right === null) {
// 当子节点数量 = 0 / 1 时, child = null / 该子节点
const child = cur.left !== null ? cur.left : cur.right;
// 删除节点 cur
if (cur !== this.root) {
if (pre.left === cur) pre.left = child;
else pre.right = child;
} else {
// 若删除节点为根节点,则重新指定根节点
this.root = child;
}
}
// 子节点数量 = 2
else {
// 获取中序遍历中 cur 的下一个节点
let tmp = cur.right;
while (tmp.left !== null) {
tmp = tmp.left;
}
// 递归删除节点 tmp
this.remove(tmp.val);
// 用 tmp 覆盖 cur
cur.val = tmp.val;
}
}
AVL 树
一种
严格平衡二叉搜索树。通过旋转,能够在不影响二叉树的中序遍历序列的前提下,使失衡节点重新恢复平衡。既能保持 “二叉搜索树” 的性质,也能使树重新变为 “平衡二叉树”
叶子节点为实际存储数据的节点,包含数据、左右子指针和高度信息,其左右子节点均为空指针 (null)
适合对查找性能要求极高,而插入 / 删除操作相对较少的场景
右旋
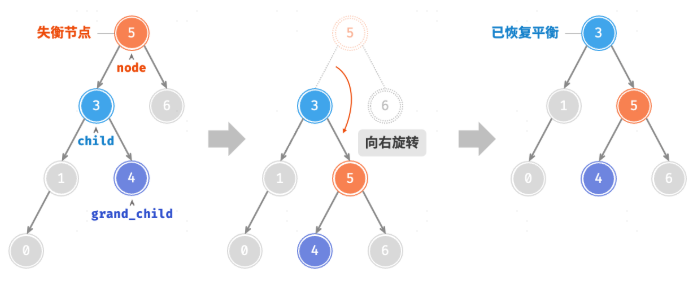
1
2
3
4
5
6
7
8
9
10
11
12
13/* 右旋操作 */
#rightRotate(node) {
const child = node.left;
const grandChild = child.right;
// 以 child 为原点,将 node 向右旋转
child.right = node;
node.left = grandChild;
// 更新节点高度
this.#updateHeight(node);
this.#updateHeight(child);
// 返回旋转后子树的根节点
return child;
}左旋
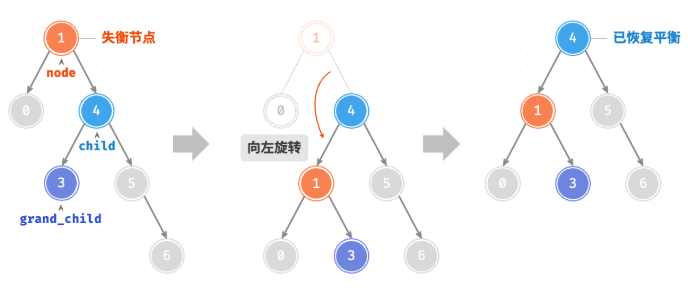
1
2
3
4
5
6
7
8
9
10
11
12
13/* 左旋操作 */
#leftRotate(node) {
const child = node.right;
const grandChild = child.left;
// 以 child 为原点,将 node 向左旋转
child.left = node;
node.right = grandChild;
// 更新节点高度
this.#updateHeight(node);
this.#updateHeight(child);
// 返回旋转后子树的根节点
return child;
}先左旋后右旋
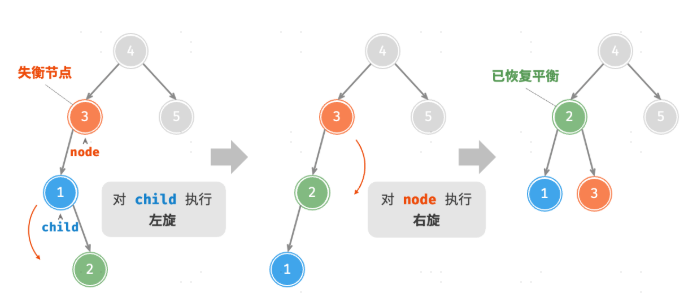
先右旋后左旋
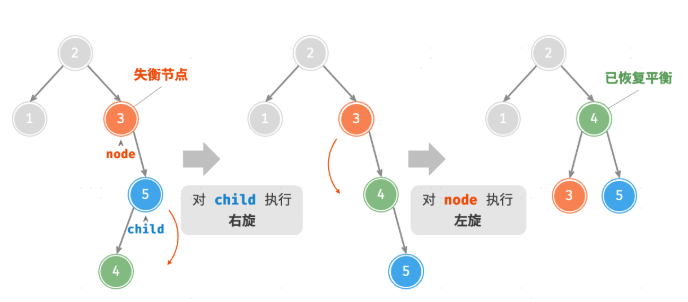
| 失衡节点的平衡因子 | 子节点的平衡因子 | 应采用的旋转方法 |
|---|---|---|
| > 1 (左偏树 LL 型失衡) | >= 0 | 右旋 |
| > 1 (左偏树 LR 型失衡) | < 0 | 先左旋后右旋 |
| < -1 (右偏树 RR 型失衡) | <= 0 | 左旋 |
| < -1 (右偏树 RL 型失衡) | > 0 | 先右旋后左旋 |
1 | /* 执行旋转操作,使该子树重新恢复平衡 */ |
红黑树
一种
近似平衡的二叉搜索树,通过一组规则维护树的 “近似平衡”,确保插入、删除、查找操作的时间复杂度始终保持在 O(logn)
叶子节点为虚拟的哨兵节点 (NIL)。所有 “实际存储数据的节点” 都必须有两个子节点,即使某个子节点在逻辑上不存在。为了满足这一要求,红黑树引入了虚拟的叶子节点 (NIL 节点),它们是不存储数据的黑色节点,用于替代空指针,简化边界逻辑
动态数据场景,如频繁增删中效率更高
特性
- 节点非黑即红
- 根节点一定是黑色
- 叶子节点(NIL)一定是黑色
- 每个红色节点的两个子节点都为黑色 (从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 黑色完美平衡:从任一节点到其每个叶子的所有路径,都包含相同数目的黑色节点
- 插入红黑树节点,先设置为红色
- 特性 5 为平衡条件
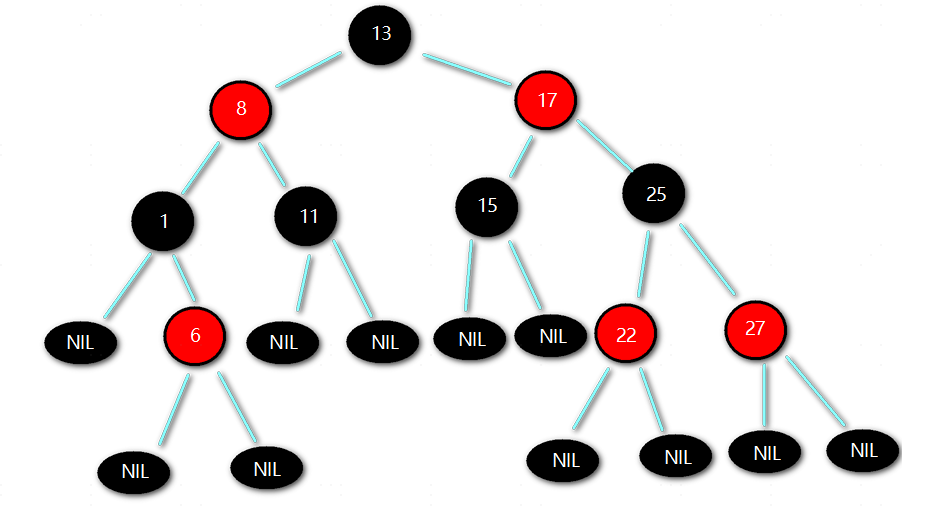
恢复平衡
- 变色
- 左旋/右旋
堆
满足特定条件的
完全二叉树,分为大根堆和小根堆
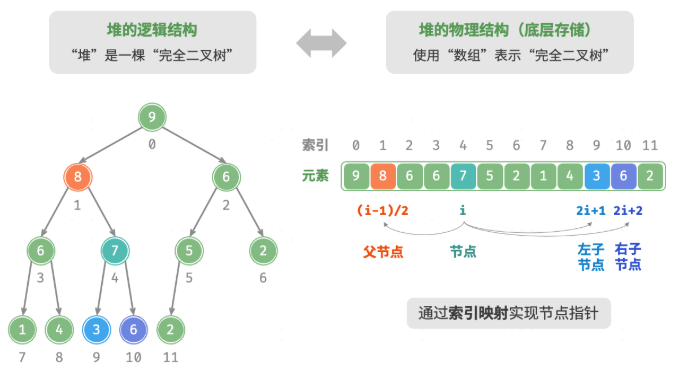
- 堆的存储与表示:数组
- 访问堆顶元素:列表的首个元素
- 元素入堆:添加到堆底,然后从底至顶执行堆化(heapify),比较插入节点与其父节点的值,如果插入节点更大/小,则将它们交换。复杂度为 O(logn)
- 堆顶元素出堆:O(logn)
- 交换堆顶元素与堆底元素(交换根节点与最右叶节点)
- 交换完成后,将堆底元素从列表中删除
- 从根节点开始,从顶至底执行堆化:将根节点的值与其两个子节点的值进行比较,将最大的子节点与根节点交换
建堆
- 方法一:借助入堆操作实现。依次对每个元素执行入堆操作,复杂度为 O(nlogn)
- 方法一:通过遍历堆化实现。复杂度为 O(n),分为两步
- 将列表所有元素原封不动地添加到堆中,此时堆的性质尚未得到满足
- 倒序遍历堆 (层序遍历的倒序),依次对每个非叶节点 (叶子节点没有子节点无需向下堆化)执行
从顶至底堆化
Top-K 问题
- 初始化一个小顶堆,其堆顶元素最小
- 先将数组的前 k 个元素依次入堆
- 从第 k + 1 个元素开始,若当前元素大于堆顶元素,则将堆顶元素出堆,并将当前元素入堆
- 遍历完成后,堆中保存的就是最大的 k 个元素,复杂度为 O(nlogk)
1 | /* 元素入堆 */ |
常见应用
- 优先队列:堆通常作为实现优先队列的首选数据结构,其入队和出队操作的时间复杂度均为 O(logn),建堆操作为 O(n),非常高效
- 堆排序:给定一组数据,可以用它们建立一个堆,然后不断地执行元素出堆操作,从而得到有序数据
- 获取最大的 k 个元素:一个经典的算法问题,例如选择热度前 10 的新闻作为微博热搜,选取销量前 10 的商品等
图
一种非线性数据结构,由顶点(vertex)和边(edge)组成。可以将图 G 抽象地表示为一组顶点 V 和一组边 E 的集合
1 | V = {1, 2, 3, 4, 5} |
图的表示
以下以无向图举例
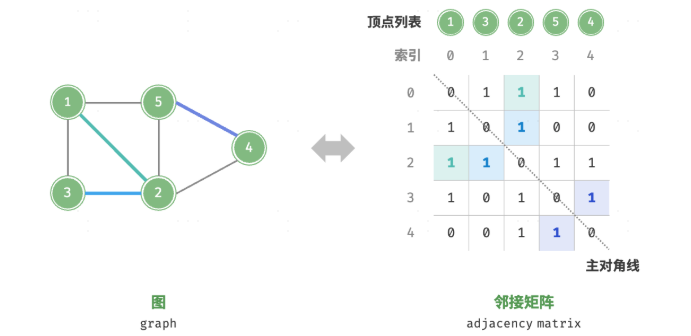
邻接矩阵
顶点数量为 n,邻接矩阵(adjacency matrix)使用一个 n * n 大小的矩阵来表示图,每一行(列)代表一个顶点,矩阵元素代表边,用 1 或 0 表示两个顶点之间是否存在边,替换为权重则可表示有权图
可以直接访问矩阵元素以获取边,因此增删查改操作的效率很高,时间复杂度均为 O(1)。然而,矩阵的空间复杂度为 O(n ^ 2),内存占用较多
- 添加或删除边:O(1) 直接在邻接矩阵中修改指定的边,无向图需要同时更新两个方向的边
- 添加顶点:O(n) 在邻接矩阵的尾部添加一行一列,并全部填 0
- 删除顶点:O(n ^ 2) 在邻接矩阵中删除一行一列,当删除首行首列时达到最差情况,需要将 (n - 1 ) ^ 2 个元素 “向左上移动”
- 初始化:传入 n 个顶点,初始化长度为 n 的顶点列表 ,使用 O(n) 时间;初始化 n ^ 2 大小的邻接矩阵,使用 O(n ^ 2) 时间
1 | /* 基于邻接矩阵实现的无向图类 */ |
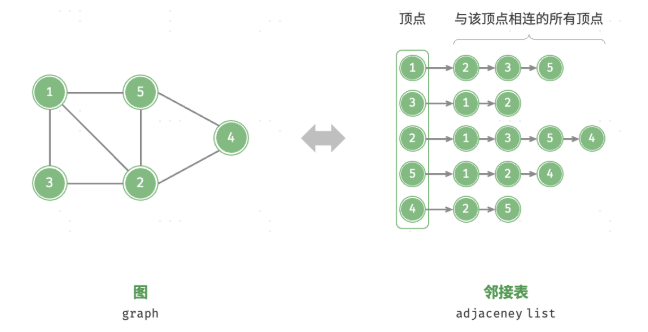
邻接表
使用 n 个链表来表示图,链表节点表示顶点。第 i 个链表对应顶点 i,其中存储了该顶点的所有邻接顶点(与该顶点相连的顶点)。并可以在特定情况下将链表优化成 AVL 树或哈希表,降低复杂度
设无向图的顶点总数为 n、边总数为 m
- 添加边:O(1) 在顶点对应链表的末尾添加边,无向图需要同时添加两个方向的边
- 删除边:O(m) 在顶点对应链表中查找并删除指定边,无向图需要同时删除两个方向的边
- 添加顶点:O(1) 在邻接表中添加一个链表,并将新增顶点作为链表头节点
- 删除顶点:O(n + m) 遍历整个邻接表,删除包含指定顶点的所有边
- 初始化:O(n + m) 在邻接表中创建 n 个顶点和 2m 条边
1 | /* 基于邻接表实现的无向图类 */ |
| 邻接矩阵 | 邻接表 (链表) | 邻接表 (哈希表) | |
|---|---|---|---|
| 判断是否邻接 | O(1) | O(n) | O(1) |
| 添加边 | O(1) | O(1) | O(1) |
| 删除边 | O(1) | O(n) | O(1) |
| 添加顶点 | O(n) | O(1) | O(1) |
| 删除顶点 | O(n ^ 2) | O(n + m) | O(n) |
| 内存空间占用 | O(n ^ 2) | O(n + m) | O(n + m) |
图的遍历
广度优先遍历
由近及远的遍历,从某个节点出发,始终优先访问距离最近的顶点,并一层层向外扩张
- 将遍历起始顶点 startVet 加入队列,并开启循环
- 在循环的每轮迭代中,弹出队首顶点并记录访问,然后将该顶点的所有邻接顶点加入到队列尾部
- 循环步骤 2. ,直到所有顶点被访问完毕后结束,时间复杂度为 O(n + m),空间复杂度为 O(n)
1 | // 使用邻接表来表示图,以便获取指定顶点的所有邻接顶点 |
深度优先遍历
由顶到底的遍历,时间复杂度为 O(n + m),空间复杂度为 O(n)
1 | /* 深度优先遍历 */ |
内存与缓存
计算机中包括三种类型的存储设备:硬盘(hard disk)、内存(random-access memory, RAM)、缓存(cache memory)
数据结构的内存效率
- 内存是有限的,且同一块内存不能被多个程序共享
- 随着反复申请与释放内存,空闲内存的碎片化程度会越来越高
数据结构的缓存效率
CPU 从缓存中成功获取数据的比例称为
缓存命中率(cache hit rate),通常用来衡量缓存效率。为了尽可能达到更高的效率,缓存会采取以下数据加载机制
- 缓存行:缓存不是单个字节地存储与加载数据,而是以缓存行为单位。相比于单个字节的传输,缓存行的传输形式更加高效
- 预取机制:处理器会尝试预测数据访问模式(例如顺序访问、固定步长跳跃访问等),并根据特定模式将数据加载至缓存之中
- 空间局部性:如果一个数据被访问,那么它附近的数据可能近期也会被访问。因此,缓存在加载某一数据时,也会加载其附近的数据
- 时间局部性:如果一个数据被访问,那么它在不久的将来很可能再次被访问。缓存利用这一原理,通过保留最近访问过的数据来提高命中率






